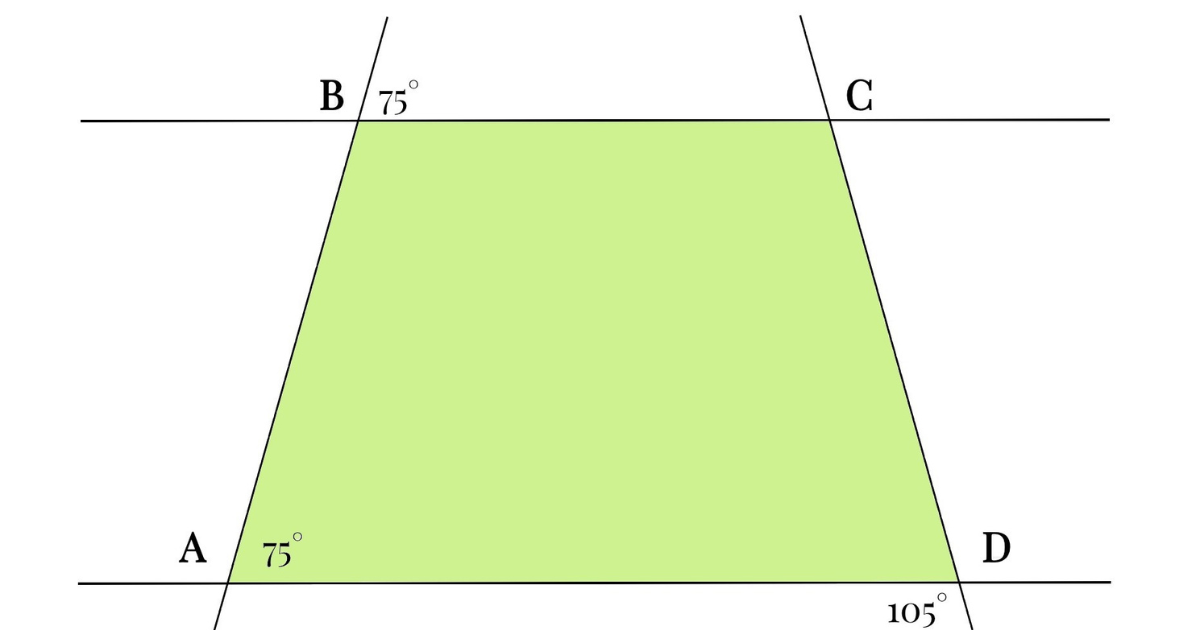
When it comes to understanding the angles in a quadrilateral, particularly the measure of angle ∠ADC in quadrilateral ABCD, it can be quite fascinating. Whether you’re a student trying to get a grasp of geometry or simply someone interested in how shapes work, this blog will walk you through the essential concepts in a straightforward way.
What Is A Quadrilateral?
Before diving into the specific angle ∠ADC, let’s start with the basics. A quadrilateral is a polygon with four sides, four vertices, and four angles. The sum of the interior angles of any quadrilateral is always 360 degrees. This rule is fundamental in geometry and helps us solve various problems related to quadrilaterals.
Key Properties Of Quadrilaterals
To understand the measure of ∠ADC, it’s crucial to grasp a few key properties of quadrilaterals:
- Sum of Angles: As mentioned earlier, the sum of all interior angles in a quadrilateral is 360 degrees.
- Types of Quadrilaterals: Quadrilaterals can be categorized into different types based on their properties, such as squares, rectangles, parallelograms, rhombuses, and trapezoids. Each type has unique characteristics affecting the measures of its angles.
Analyzing Angle ∠ADC
In a general quadrilateral ABCD, the measure of angle ∠ADC is not something you can calculate directly without additional information. The reason is that there are multiple types of quadrilaterals, and each type has different properties and constraints. To find the measure of ∠ADC, you often need more specific details about the quadrilateral.
1. For General Quadrilaterals: In a general quadrilateral, if you know the measures of the other three angles (say ∠ABC, ∠BCD, and ∠DAB), you can calculate ∠ADC by using the fact that the sum of all angles is 360 degrees. Here’s how:
Measure of ∠ADC=360∘−(Measure of ∠ABC+Measure of ∠BCD+Measure of ∠DAB)\text{Measure of } ∠ADC = 360^\circ – (\text{Measure of } ∠ABC + \text{Measure of } ∠BCD + \text{Measure of } ∠DAB)Measure of ∠ADC=360∘−(Measure of ∠ABC+Measure of ∠BCD+Measure of ∠DAB)
For Special Quadrilaterals:
- Rectangle or Square: In a rectangle or square, all angles are right angles (90 degrees). Thus, each angle, including ∠ADC, measures 90 degrees.
- Parallelogram: In a parallelogram, opposite angles are equal. If you know one angle, you can find the measure of ∠ADC if you know its opposite angle.
- Rhombus: In a rhombus, opposite angles are equal, and the sum of adjacent angles is always 180 degrees. This means if you know one angle, you can easily find the measure of ∠ADC.
- Trapezoid: In a trapezoid (or trapezium), if you know the measures of the two non-parallel angles, you can find the remaining angles using the property that the sum of angles in a quadrilateral is 360 degrees.
Examples
Let’s consider a few examples to illustrate how you can find the measure of ∠ADC.
Example 1: General Quadrilateral
Suppose you have a quadrilateral ABCD where ∠ABC = 85 degrees, ∠BCD = 95 degrees, and ∠DAB = 100 degrees. To find ∠ADC, use the formula:
Measure of ∠ADC=360∘−(85∘+95∘+100∘)=360∘−280∘=80∘\text{Measure of } ∠ADC = 360^\circ – (85^\circ + 95^\circ + 100^\circ) = 360^\circ – 280^\circ = 80^\circMeasure of ∠ADC=360∘−(85∘+95∘+100∘)=360∘−280∘=80∘
So, ∠ADC = 80 degrees.
Example 2: Rectangle
In a rectangle ABCD, all angles are right angles. Therefore, ∠ADC, like all other angles, measures 90 degrees.
Example 3: Parallelogram
Consider a parallelogram ABCD where ∠ABC = 120 degrees. Since opposite angles in a parallelogram are equal, ∠ADC = ∠ABC = 120 degrees.
Practical Applications
Understanding how to measure angles in a quadrilateral has real-world applications. For instance:
- Architecture and Design: Accurate measurements of angles are essential in designing buildings and structures to ensure they are stable and functional.
- Engineering: In fields like civil engineering, knowledge of angles in various shapes is crucial for construction projects.
- Everyday Problem Solving: From assembling furniture to planning layouts, understanding angles helps in making precise decisions.
Summary
The measure of angle ∠ADC in quadrilateral ABCD depends on the specific type of quadrilateral and the measures of the other angles. By knowing some basic properties and using simple calculations, you can find ∠ADC effectively. Remember that while the sum of angles in any quadrilateral is always 360 degrees, special types of quadrilaterals have their own unique angle properties that simplify the process.